如图, 在直角坐标系中,矩形ABCD的边BC在X轴上,点B、D的坐标分别为B(1,0),D(3,3).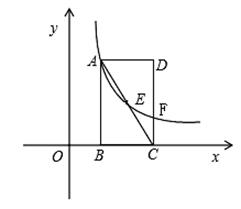
(1)直接写出点C的坐标;
(2)若反比例函数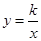 的图象经过直线AC上的点E,且点E的坐标为(2,m),求
的图象经过直线AC上的点E,且点E的坐标为(2,m),求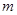 的值及反比例函数的解析式;
的值及反比例函数的解析式;
(3)若(2)中的反比例函数的图象与CD相交于点F,连接 EF,在线段AB上(端点除外)找一点P,使得:S△PEF=S△CEF,并求出点P的坐标.
相关知识点
推荐套卷
如图, 在直角坐标系中,矩形ABCD的边BC在X轴上,点B、D的坐标分别为B(1,0),D(3,3).
(1)直接写出点C的坐标;
(2)若反比例函数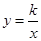 的图象经过直线AC上的点E,且点E的坐标为(2,m),求
的图象经过直线AC上的点E,且点E的坐标为(2,m),求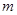 的值及反比例函数的解析式;
的值及反比例函数的解析式;
(3)若(2)中的反比例函数的图象与CD相交于点F,连接 EF,在线段AB上(端点除外)找一点P,使得:S△PEF=S△CEF,并求出点P的坐标.