设集合W是满足下列两个条件的无穷数列{an}的集合：
①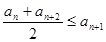
②
，其中n∈N*，M是与n无关的常数
(1)若{an}是等差数列，Sn是其前n项的和，a3=4，S3=18，试探究{Sn}与集合W之间的关系；
(2)设数列{bn}的通项为bn=5n-2n，且{bn}∈W，M的最小值为m，求m的值；
(3)在(2)的条件下，设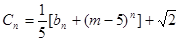
，求证：数列{Cn}中任意不同的三项都不能成为等比数列．
相关试题
的最大值。
(0≤θ<π)和
( t ∈R)，求它们的交点坐标．
的特征值
所对应的一个特征向量。
对应变换下变为点B(1，2)，求M－1.推荐套卷
设集合W是满足下列两个条件的无穷数列{an}的集合：
①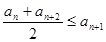 ②，其中n∈N*，M是与n无关的常数
(1)若{an}是等差数列，Sn是其前n项的和，a3=4，S3=18，试探究{Sn}与集合W之间的关系；
(2)设数列{bn}的通项为bn=5n-2n，且{bn}∈W，M的最小值为m，求m的值；
(3)在(2)的条件下，设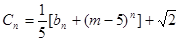，求证：数列{Cn}中任意不同的三项都不能成为等比数列．
粤公网安备 44130202000953号