如图,一次函数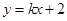 的图象与反比例函数
的图象与反比例函数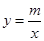 的图象交于点P,点P在第一象限.PA⊥x轴于点A,PB⊥y轴于点B.一次函数的图象分别交
的图象交于点P,点P在第一象限.PA⊥x轴于点A,PB⊥y轴于点B.一次函数的图象分别交 轴、
轴、 轴于点C、D,且S△PBD=4,
轴于点C、D,且S△PBD=4, .
.求点D的坐标;
求一次函数与反比例函数解析式;
根据图象写出一次函数的值大于反比例函数的值的
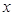 的取值范围.
的取值范围.
推荐套卷
如图,一次函数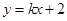 的图象与反比例函数
的图象与反比例函数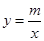 的图象交于点P,点P在第一象限.PA⊥x轴于点A,PB⊥y轴于点B.一次函数的图象分别交
的图象交于点P,点P在第一象限.PA⊥x轴于点A,PB⊥y轴于点B.一次函数的图象分别交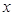 轴、
轴、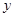 轴于点C、D,且S△PBD=4,
轴于点C、D,且S△PBD=4, .
.求点D的坐标;
求一次函数与反比例函数解析式;
根据图象写出一次函数的值大于反比例函数的值的
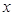 的取值范围.
的取值范围.