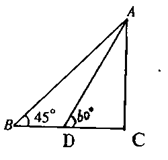
如图,在广场上用氢气球悬挂着“人文黔东南,和谐黔东南,美丽黔东南,建设黔东南”的大型宣传条幅AC、小明站在B处看条幅顶端A的仰角为45o,再往条幅方向前往20米到D处,在D处看条幅顶端A的仰角为60o,求条幅AC的高度(小明的身高不计,条幅垂直于地面)(结果精确到0.1米,参考数据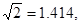
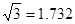 )
)
相关知识点
推荐套卷
如图,在广场上用氢气球悬挂着“人文黔东南,和谐黔东南,美丽黔东南,建设黔东南”的大型宣传条幅AC、小明站在B处看条幅顶端A的仰角为45o,再往条幅方向前往20米到D处,在D处看条幅顶端A的仰角为60o,求条幅AC的高度(小明的身高不计,条幅垂直于地面)(结果精确到0.1米,参考数据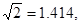
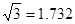 )
)