一支车队有15辆车，某天依次出发执行运输任务，第一辆车于下午2时出发，第二辆车于下午2时10分出发，第三辆车于下午2时20分出发，依此类推。假设所有的司机都连续开车，并都在下午6时停下来休息。
（1）到下午6时最后一辆车行驶了多长时间？
（2）如果每辆车的行驶速度都是60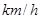
，这个车队当天一共行驶了多少千米?
相关试题
|x+1|.
-x)，求其定义域，并判断其奇偶性、单调性.相关知识点
推荐套卷
一支车队有15辆车，某天依次出发执行运输任务，第一辆车于下午2时出发，第二辆车于下午2时10分出发，第三辆车于下午2时20分出发，依此类推。假设所有的司机都连续开车，并都在下午6时停下来休息。
（1）到下午6时最后一辆车行驶了多长时间？
（2）如果每辆车的行驶速度都是60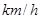，这个车队当天一共行驶了多少千米?
粤公网安备 44130202000953号