如图，在平行六面体ABCD-A1B1C1D1中，四边形ABCD与四边形CC1D1D均是边长为1的正方形，∠ADD1="120°" ，点E为A1B1的中点，点P，Q分别是BD，CD1上的动点，且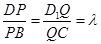
.
（1）当平面PQE//平面ADD1A1时，求
的值.
（2）在（1）的条件下，求直线QE与平面DQP所成角的正弦值.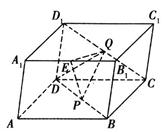
（
的一条对称轴为直线
（Ⅰ）求
（Ⅱ）用五点法画出函数
上的简图．
是平面坐标内三点，其坐标分别为
，
，
．
和
大小，并判断
形状；
为
中点，求
．
.（Ⅰ） 求
的值；（Ⅱ） 求
的值．
，
与
夹角为
（Ⅰ）若
（Ⅱ）若
与
的终边与单位圆交于点
（Ⅰ）求出
、
、
的值；（Ⅱ）求
的值．相关知识点
推荐套卷
如图，在平行六面体ABCD-A1B1C1D1中，四边形ABCD与四边形CC1D1D均是边长为1的正方形，∠ADD1="120°" ，点E为A1B1的中点，点P，Q分别是BD，CD1上的动点，且.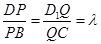
（1）当平面PQE//平面ADD1A1时，求的值.
（2）在（1）的条件下，求直线QE与平面DQP所成角的正弦值.
粤公网安备 44130202000953号