如图,P是反比例函数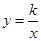 (
(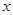 >0)的图象上的一点,PN垂直
>0)的图象上的一点,PN垂直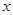 轴于点N,PM
轴于点N,PM
垂直y轴于点M,矩形OMPN的面积为2,且ON=1,一次函数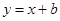 的图象经过点P.
的图象经过点P.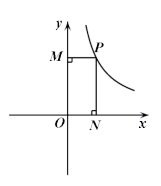
(1)求该反比例函数和一次函数的解析式;
(2)设直线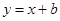 与
与 轴的交点为A,点Q在y轴上,当△QOA的面积等于矩形OMPN的面积的
轴的交点为A,点Q在y轴上,当△QOA的面积等于矩形OMPN的面积的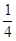 时,直接写出点Q的坐标.
时,直接写出点Q的坐标.
相关知识点
推荐套卷
如图,P是反比例函数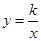 (
(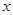 >0)的图象上的一点,PN垂直
>0)的图象上的一点,PN垂直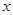 轴于点N,PM
轴于点N,PM
垂直y轴于点M,矩形OMPN的面积为2,且ON=1,一次函数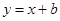 的图象经过点P.
的图象经过点P.
(1)求该反比例函数和一次函数的解析式;
(2)设直线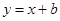 与
与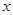 轴的交点为A,点Q在y轴上,当△QOA的面积等于矩形OMPN的面积的
轴的交点为A,点Q在y轴上,当△QOA的面积等于矩形OMPN的面积的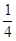 时,直接写出点Q的坐标.
时,直接写出点Q的坐标.