1已知函数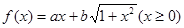 ,
,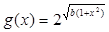 ,
,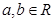 ,且
,且 ,
, .
.
(1)求 、
、 的解析式;
的解析式;
(2)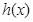 为定义在
为定义在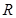 上的奇函数,且满足下列性质:①
上的奇函数,且满足下列性质:① 对一切实数
对一切实数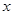 恒成立;②当
恒成立;②当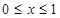 时
时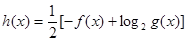 .
.
(ⅰ)求当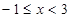 时,函数
时,函数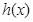 的解析式;
的解析式;
(ⅱ)求方程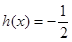 在区间
在区间 上的解的个数.
上的解的个数.
相关知识点
推荐套卷
1已知函数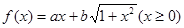 ,
,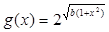 ,
,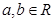 ,且
,且 ,
, .
.
(1)求 、
、 的解析式;
的解析式;
(2)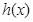 为定义在
为定义在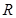 上的奇函数,且满足下列性质:①
上的奇函数,且满足下列性质:① 对一切实数
对一切实数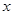 恒成立;②当
恒成立;②当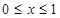 时
时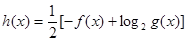 .
.
(ⅰ)求当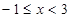 时,函数
时,函数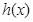 的解析式;
的解析式;
(ⅱ)求方程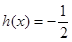 在区间
在区间 上的解的个数.
上的解的个数.