观察等式: 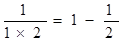 ,
,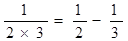 ,
, ,
,
将以上三个等式两边分别相加得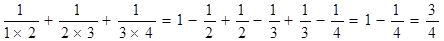 .
.
(1)猜想并写出: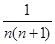 =____________________.
=____________________.
(2)直接写出下式的计算结果: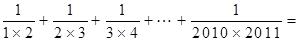 __________________________.
__________________________.
(3)探究并计算: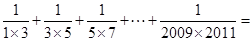 ______________________.
______________________.
相关知识点
推荐套卷
观察等式: 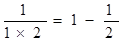 ,
,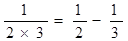 ,
, ,
,
将以上三个等式两边分别相加得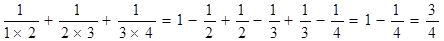 .
.
(1)猜想并写出: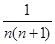 =____________________.
=____________________.
(2)直接写出下式的计算结果: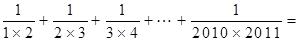 __________________________.
__________________________.
(3)探究并计算: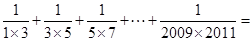 ______________________.
______________________.