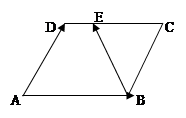在边长为1的菱形ABCD中,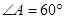 ,E是线段CD上一点,满足
,E是线段CD上一点,满足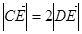 ,如图.设
,如图.设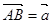 ,
,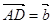 .
.
(1)用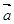 、
、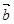 表示
表示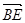 ;
;
(2)在线段BC上是否存在一点F满足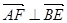 ?若存在,判定F点的位置,并求
?若存在,判定F点的位置,并求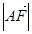 ;若不存在,请说明理由
;若不存在,请说明理由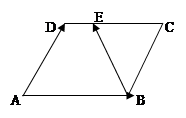
相关知识点
推荐套卷
在边长为1的菱形ABCD中,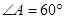 ,E是线段CD上一点,满足
,E是线段CD上一点,满足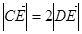 ,如图.设
,如图.设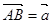 ,
,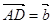 .
.
(1)用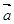 、
、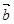 表示
表示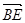 ;
;
(2)在线段BC上是否存在一点F满足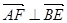 ?若存在,判定F点的位置,并求
?若存在,判定F点的位置,并求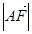 ;若不存在,请说明理由
;若不存在,请说明理由