在某次试验中,有两个试验数据x,y,统计的结果如下面的表格1.
| x |
1 |
2 |
3 |
4 |
5 |
| y |
2 |
3 |
4 |
4 |
5 |



(1)在给出的坐标系中画出x,y的散点图。
(2)补全表格2,然后根据表格2的内容和公式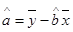 ,
,

1求出y对x的回归直线方程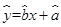 中回归系数
中回归系数
2估计当x为10时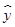 的值是多少?
的值是多少?
相关知识点
推荐套卷
在某次试验中,有两个试验数据x,y,统计的结果如下面的表格1.
| x |
1 |
2 |
3 |
4 |
5 |
| y |
2 |
3 |
4 |
4 |
5 |



(1)在给出的坐标系中画出x,y的散点图。
(2)补全表格2,然后根据表格2的内容和公式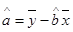 ,
,

1求出y对x的回归直线方程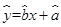 中回归系数
中回归系数
2估计当x为10时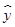 的值是多少?
的值是多少?