请阅读材料并填空:
问题:如图1,在等边三角形ABC内有一点P,且PA=2,PB=,PC=1.求∠BPC的度数和等边三角形ABC的边长.
李明同学的思路是:将△BPC绕点B顺时针旋转60°,画出旋转后的图形(如图2).连结PP′.
根据李明同学的思路,进一步思考后可求得∠BPC=____°,等边△ABC的边长为____.请你参考李明同学的思路,探究并解决下列问题:如图3,在正方形ABCD内有一点P,且PA=,BP=,PC=1.求∠BPC的度数和正方形ABCD的边长.

相关知识点
推荐套卷
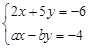 和
和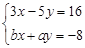 的解相同,求代数式
的解相同,求代数式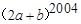 的值。
的值。 .
.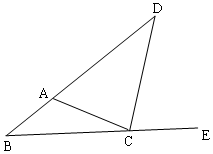

 个图形中有个三角形(用
个图形中有个三角形(用
 粤公网安备 44130202000953号
粤公网安备 44130202000953号