如图，将边长为4的正方形置于平面直角坐标系第一象限，使AB边落在x轴正半轴上，且A点的坐标是（1，0）．
（1）直线
经过点C，且与x轴交于点E，求四边形AECD的面积；
（2）若直线l经过点E，且将正方形ABCD分成面积相等的两部分，求直线l的解析式；
（3）若直线l1经过点F（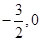
）且与直线y=3x平行．将（2）中直线l沿着y轴向上平移1个单位，交x轴于点M，交直线l1于点N，求△NMF的面积．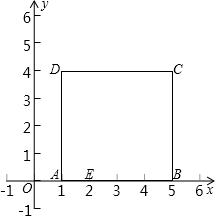
如图，将边长为4的正方形置于平面直角坐标系第一象限，使AB边落在x轴正半轴上，且A点的坐标是（1，0）．
（1）直线经过点C，且与x轴交于点E，求四边形AECD的面积；
（2）若直线l经过点E，且将正方形ABCD分成面积相等的两部分，求直线l的解析式；
（3）若直线l1经过点F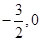（）且与直线y=3x平行．将（2）中直线l沿着y轴向上平移1个单位，交x轴于点M，交直线l1于点N，求△NMF的面积．
的两根之比为 
，求 
的值。
的两根分别是
，求
的两根的平方.
是方程 
的两根，不解方程，求下列各式的值：
；②
；③
；④
.
粤公网安备 44130202000953号