如图，直线y=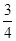
x+6与x轴、y轴分别相交于点E、F，点A的坐标为（﹣6，0），P（x，y）是直线y=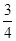x+6上一个动点．
（1）在点P运动过程中，试写出△OPA的面积s与x的函数关系式；
（2）当P运动到什么位置，△OPA的面积为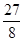
，求出此时点P的坐标；
（3）过P作EF的垂线分别交x轴、y轴于C、D．是否存在这样的点P，使△COD≌△FOE？若存在，直接写出此时点P的坐标（不要求写解答过程）；若不存在，请说明理由．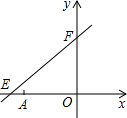
相关试题
如图，直线y=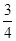x+6与x轴、y轴分别相交于点E、F，点A的坐标为（﹣6，0），P（x，y）是直线y=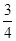x+6上一个动点．
（1）在点P运动过程中，试写出△OPA的面积s与x的函数关系式；
（2）当P运动到什么位置，△OPA的面积为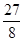，求出此时点P的坐标；
（3）过P作EF的垂线分别交x轴、y轴于C、D．是否存在这样的点P，使△COD≌△FOE？若存在，直接写出此时点P的坐标（不要求写解答过程）；若不存在，请说明理由．
．
，则
；
．
．
．
．
x+2分别交y轴、x轴于A、B两点，抛物线y=－
+bx+c过A、B两点．
粤公网安备 44130202000953号