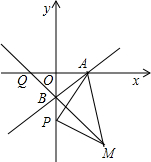
已知：如图，平面直角坐标系xOy中，点A、B的坐标分别为A（4，0），B（0，﹣4），P为y轴上B点下方一点，PB=m（m＞0），以AP为边作等腰直角三角形APM，其中PM=PA，点M落在第四象限．
（1）求直线AB的解析式；
（2）用m的代数式表示点M的坐标；
（3）若直线MB与x轴交于点Q，判断点Q的坐标是否随m的变化而变化，写出你的结论并说明理由．