国家教育部规定“中小学生每天在校体育活动时间不低于1小时”.某中学为了了解学生体育活动情况,随机抽查了520名毕业班学生,调查内容是:“每天锻炼是否超过1小时及未超过1小时的原因”.以下是根据所得的数据制成的统计图的一部分.
根据以上信息,解答下列问题:每天在校锻炼时间超过1小时的人数是 ;
请将图2补充完整;
2010年我市初中毕业生约为9.6万人,请你估计今年全市初中毕业生中每天锻炼时间超过1小时的学生约有多少万人?


相关知识点
推荐套卷
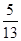 ,BC=26.
,BC=26.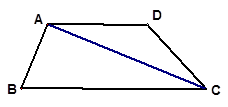

 的外接圆,
的外接圆,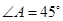 ,
, 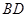 为⊙O的直径,BD=2,连结
为⊙O的直径,BD=2,连结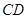 ,求BC的长.
,求BC的长. 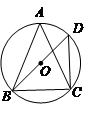
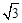 ,点B为CD延长线上一点,且BD=2AD.求AB的长.
,点B为CD延长线上一点,且BD=2AD.求AB的长.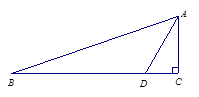
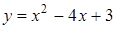
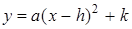 的形式;
的形式;
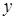 随着
随着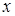 的增大而减小?
的增大而减小? 粤公网安备 44130202000953号
粤公网安备 44130202000953号