设数列 的前n项和为
的前n项和为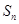 ,
,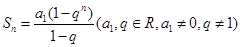
(1)求证:数列 是等比数列;
是等比数列;
(2)若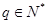 ,是否存在q的某些取值,使数列
,是否存在q的某些取值,使数列 中某一项能表示为另外三项之和?若能求出q的全部取值集合,若不能说明理由。
中某一项能表示为另外三项之和?若能求出q的全部取值集合,若不能说明理由。
(3)若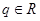 ,是否存在
,是否存在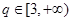 ,使数列
,使数列 中,某一项可以表示为另外三项之和?若存在指出q的一个取值,若不存在,说明理由。
中,某一项可以表示为另外三项之和?若存在指出q的一个取值,若不存在,说明理由。
相关知识点
推荐套卷
设数列 的前n项和为
的前n项和为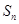 ,
,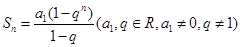
(1)求证:数列 是等比数列;
是等比数列;
(2)若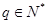 ,是否存在q的某些取值,使数列
,是否存在q的某些取值,使数列 中某一项能表示为另外三项之和?若能求出q的全部取值集合,若不能说明理由。
中某一项能表示为另外三项之和?若能求出q的全部取值集合,若不能说明理由。
(3)若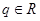 ,是否存在
,是否存在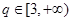 ,使数列
,使数列 中,某一项可以表示为另外三项之和?若存在指出q的一个取值,若不存在,说明理由。
中,某一项可以表示为另外三项之和?若存在指出q的一个取值,若不存在,说明理由。