小明想利用太阳光测量楼高.他带着皮尺来到一栋楼下,发现对面墙上有这栋楼的影子,针对这种情况,他设计了一种测量方案,具体测量情况如下:
如示意图,小明边移动边观察,发现站到点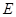 处时,可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠,且高度恰好相同.此时,测得小明落在墙上的影子高度CD=1.2m,CE=0.8m,CA=30m(点
处时,可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠,且高度恰好相同.此时,测得小明落在墙上的影子高度CD=1.2m,CE=0.8m,CA=30m(点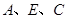 在同一直线上).
在同一直线上).
已知小明的身高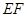 是1.7m,请你帮小明求出楼高
是1.7m,请你帮小明求出楼高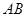 (结果精确到0.1m).
(结果精确到0.1m).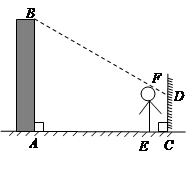
小明想利用太阳光测量楼高.他带着皮尺来到一栋楼下,发现对面墙上有这栋楼的影子,针对这种情况,他设计了一种测量方案,具体测量情况如下:
如示意图,小明边移动边观察,发现站到点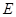 处时,可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠,且高度恰好相同.此时,测得小明落在墙上的影子高度CD=1.2m,CE=0.8m,CA=30m(点
处时,可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠,且高度恰好相同.此时,测得小明落在墙上的影子高度CD=1.2m,CE=0.8m,CA=30m(点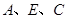 在同一直线上).
在同一直线上).
已知小明的身高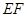 是1.7m,请你帮小明求出楼高
是1.7m,请你帮小明求出楼高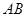 (结果精确到0.1m).
(结果精确到0.1m).