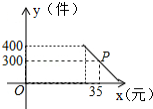
某商店购进一批进价为20元 件的日用商品,第一个月,按进价提高 的价格出售,售出400件,第二个月,商店准备在不低于原售价的基础上进行加价销售,根据销售经验,提高销售单价会导致销售量的减少.销售量 (件 与销售单价 (元 的关系如图所示.
(1)图中点 所表示的实际意义是 ;销售单价每提高1元时,销售量相应减少 件;
(2)请直接写出 与 之间的函数表达式 ;自变量 的取值范围为 ;
(3)第二个月的销售单价定为多少元时,可获得最大利润?最大利润是多少?
相关知识点
推荐套卷
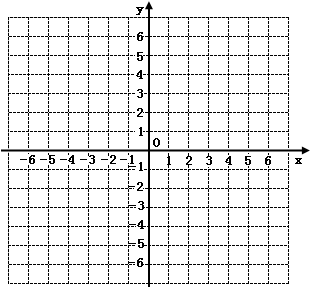
 轴是什么位置关系?
轴是什么位置关系? 、
、
 粤公网安备 44130202000953号
粤公网安备 44130202000953号