在图所示的平面直角坐标系中表示下面各点：。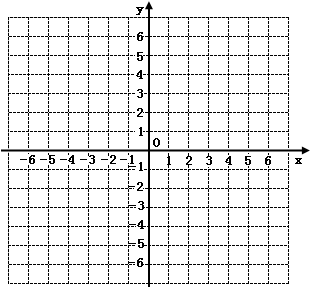
A（0，3），B（1，－3），C（3，－5），D（－3，－5），E（3，5），F（5，7）。
（1）A点到原点O的距离是__ __个单位长。
（2）将点C向左平移6个单位，它会与点 重合。
（3）连接CE，则直线CE与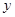
轴是什么位置关系？
（4）点F到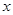
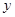、轴的距离分别是多少？
的两条对角线
、
相交于点
．图中有哪些三角形是全等的？
≥
的负整数解。
相关知识点
推荐套卷
在图所示的平面直角坐标系中表示下面各点：。
A（0，3），B（1，－3），C（3，－5），D（－3，－5），E（3，5），F（5，7）。
（1）A点到原点O的距离是__ __个单位长。
（2）将点C向左平移6个单位，它会与点 重合。
（3）连接CE，则直线CE与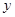轴是什么位置关系？
（4）点F到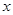、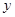轴的距离分别是多少？
粤公网安备 44130202000953号