设函数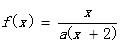
方程f(x)=x有唯一的解，
已知f(xn)=xn+1(n∈N﹡)且
(1)求证：数列{
}是等差数列；
(2)若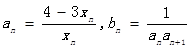
，求sn=b1+b2+b3+…+bn;
(3)在(2)的冬件下,若不等式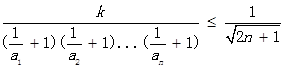
对一切n∈N﹡
均成立，求k的最大值．
，求证：不论
为何值，直线
恒过第一象限．
过定点
，且与两坐标轴围成三角形面积为
，求直线
的倾斜角是直线
的倾斜角的大小的
倍，且直线
；（2）在
轴上截距为
；（3）在
轴上截距为
．求直线
，
，
，求
中
边上中线的方程．
的方程为
，根据下列条件分别确定实数
的值．
轴上的截距为
；
．推荐套卷
设函数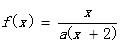方程f(x)=x有唯一的解，
已知f(xn)=xn+1(n∈N﹡)且
(1)求证：数列{}是等差数列；
(2)若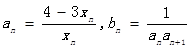，求sn=b1+b2+b3+…+bn;
(3)在(2)的冬件下,若不等式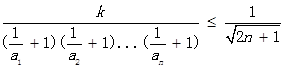对一切n∈N﹡
均成立，求k的最大值．
粤公网安备 44130202000953号