如图，在Rt△ABC中，∠C=90°，AD是∠BAC的平分线，以AB上一点O为圆心，AD为弦作⊙O． （1）求证：BC为⊙O的切线；
(2）若AC= 6，tanB=
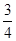，求⊙O的半径．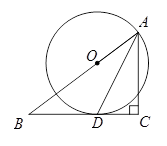
相关试题
、
在第一象限的图像，
，过
，作
轴的平行线交
，交
轴于
，若
；求双曲线
中，
． 
＞
．
．
交
轴于点
，交
轴于点
，抛物线
经过
（1，0）三点.
的坐标为（-1，0），在直线
，使
与
相似，求出点
，使
的面积等于四边形
的面积？如果存在，请求出点相关知识点
推荐套卷
如图，在Rt△ABC中，∠C=90°，AD是∠BAC的平分线，以AB上一点O为圆心，AD为弦作⊙O． （1）求证：BC为⊙O的切线；
(2）若AC= 6，tanB=
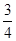，求⊙O的半径．
粤公网安备 44130202000953号