(本小题满分15分)
如图所示,一科学考察船从港口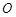 出发,沿北偏东
出发,沿北偏东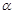 角的射线
角的射线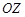 方向航行,而在离港口
方向航行,而在离港口 (
(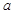 为正常数)海里的北偏东
为正常数)海里的北偏东 角的A处有一个供给科考船物资的小岛,其中
角的A处有一个供给科考船物资的小岛,其中 ,
,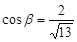 .现指挥部需要紧急征调沿海岸线港口
.现指挥部需要紧急征调沿海岸线港口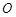 正东m(
正东m( )海里的B处的补给船,速往小岛A装运物资供给科考船,该船沿BA方向全速追赶科考船,并在C处相遇.经测算当两船运行的航向与海岸线OB围成的三角形OBC的面积最小时,这种补给最适宜.
)海里的B处的补给船,速往小岛A装运物资供给科考船,该船沿BA方向全速追赶科考船,并在C处相遇.经测算当两船运行的航向与海岸线OB围成的三角形OBC的面积最小时,这种补给最适宜.
⑴ 求S关于m的函数关系式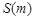 ;
;
⑵ 应征调m为何值处的船只,补给最适宜.
相关知识点
推荐套卷
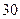 元,且每卖出一件产品,需向税务部门上交
元,且每卖出一件产品,需向税务部门上交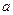 元(
元(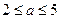 )的税收,设每件产品的日售价为
)的税收,设每件产品的日售价为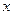 元(
元( ),根据市场调查,日销售量与
),根据市场调查,日销售量与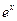 (
(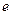 为自然对数的底数)成反比,已知每件产品的日售价为
为自然对数的底数)成反比,已知每件产品的日售价为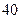 元,日销售量为
元,日销售量为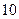 件。w.w.w..c.o.m
件。w.w.w..c.o.m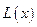 元与每件产品的日售价
元与每件产品的日售价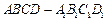 中,底面
中,底面 是直角梯形,
是直角梯形,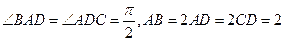
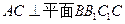
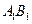 上是否存一点
上是否存一点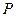 ,使得
,使得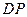 与平面
与平面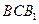 与平面
与平面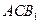 都平行?证明你的结论.
都平行?证明你的结论.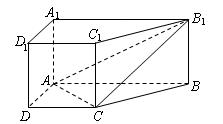
 (2)现从乙班这10名同学中随机抽取两
(2)现从乙班这10名同学中随机抽取两 名身高不低于
名身高不低于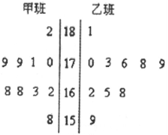
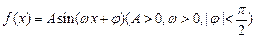 的部分图象如图所示.(Ⅰ)求函数
的部分图象如图所示.(Ⅰ)求函数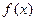 的解析式;
的解析式;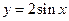 的图象通过适当的
的图象通过适当的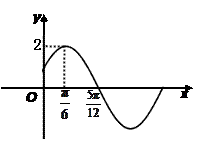 变换得到函数
变换得到函数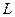 :
: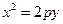 和点
和点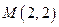 ,若抛物线
,若抛物线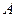 、
、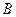 满足
满足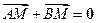 .
.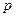 的取值范围;
的取值范围;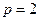 时,抛物线
时,抛物线 ,使得经过
,使得经过 粤公网安备 44130202000953号
粤公网安备 44130202000953号