(13分)已知数列{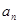 }的前n项和Sn=-
}的前n项和Sn=-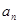 -
-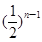 +2(n为正整数).
+2(n为正整数).
(1)令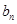 =
=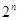
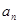 ,求证数列{
,求证数列{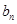 }是等差数列,并求数列{
}是等差数列,并求数列{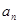 }的通项公式;
}的通项公式;
(2)令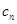 =
=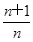
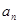 ,若Tn=c1+c2+…+cn, 求Tn。
,若Tn=c1+c2+…+cn, 求Tn。
相关知识点
推荐套卷
(13分)已知数列{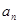 }的前n项和Sn=-
}的前n项和Sn=-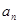 -
-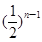 +2(n为正整数).
+2(n为正整数).
(1)令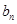 =
=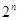
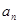 ,求证数列{
,求证数列{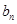 }是等差数列,并求数列{
}是等差数列,并求数列{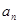 }的通项公式;
}的通项公式;
(2)令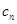 =
=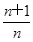
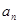 ,若Tn=c1+c2+…+cn, 求Tn。
,若Tn=c1+c2+…+cn, 求Tn。