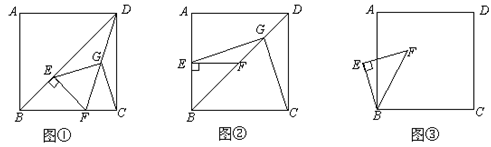
已知：如图①，正方形ABCD中，E为对角线BD上一点，
过E点作EF⊥BD交BC于F，连接DF，G为DF中点，连接EG，CG．
（1）求证：EG=CG；
（2）将图①中△BEF绕B点逆时针旋转45º，如图②所示，取DF中点G，连接EG，CG．问（1）中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由．
（3）将图①中△BEF绕B点旋转任意角度，如图③所示，再连接相应的线段，问（1）中的结论是否仍然成立？通过观察你还能得出什么结论？（均不要求证明）
相关试题
已知抛物线y＝ax2＋bx＋c经过A(－1，0)、B(3，0)、C(0，3)三点，直线l是抛物线的对称轴．
(1)求抛物线的函数关系式；
(2)设点P是直线l上的一个动点，当△PAC的周长最小时，求点P的坐标；
(3)在直线l上是否存在点M，使△MAC为等腰三角形？若存在，直接写出所有符合条件的点M的坐标；若不存在，请说明理由．
，CD＝2，求⊙O的直径．
如图，一艘巡逻艇航行至海面B处时，得知正北方向上距B处20海里的C处有一渔船发生故障，就立即指挥港口A处的救援艇前往C处营救．已知C处位于A处的北偏东45°的方向上，港口A位于B的北偏西30°的方向上．求A、C之间的距离．(结果精确到0.1海里，参考数据
≈1.41，
≈1.73)
，结果提前4天完成任务，原计划每天种多少棵树？
相关知识点
推荐套卷
粤公网安备 44130202000953号