近年来，全国房价不断上涨，某县201 0年4月份的房价平均每平方米为3600元， 比2008 年 同期的房价平均每平方米上涨了2000元，假设这两年该县房价的平均增长率均为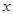
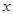，则关于的方程为( )
A． |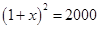
B． |
C． |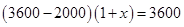
D． |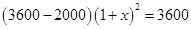
相关试题
，AB＝20.求∠A的度数.
相关知识点
推荐套卷
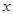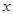近年来，全国房价不断上涨，某县201 0年4月份的房价平均每平方米为3600元， 比2008 年 同期的房价平均每平方米上涨了2000元，假设这两年该县房价的平均增长率均为，则关于的方程为( )
| A． |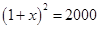
B． |
| C． |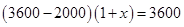
D． |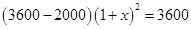
粤公网安备 44130202000953号