如图,一艘海上巡逻船在A地巡航,这时接到B地海上指挥中心紧急通知:在指挥中心北偏西60°方向的C地有一艘渔船遇险,要求马上前去救援 .此时C地位于A地北偏西30°方向上,A地位于B地北偏西75°方向上,A、B两地之间的距离为12海里 .求A、C两地之间的距离.(参考数据: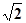 ≈1.41,
≈1.41,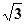 ≈1.73,
≈1.73,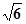 ≈2.45,结果精确到0.1).
≈2.45,结果精确到0.1).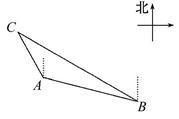
相关知识点
推荐套卷
如图,一艘海上巡逻船在A地巡航,这时接到B地海上指挥中心紧急通知:在指挥中心北偏西60°方向的C地有一艘渔船遇险,要求马上前去救援 .此时C地位于A地北偏西30°方向上,A地位于B地北偏西75°方向上,A、B两地之间的距离为12海里 .求A、C两地之间的距离.(参考数据: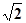 ≈1.41,
≈1.41,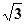 ≈1.73,
≈1.73,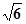 ≈2.45,结果精确到0.1).
≈2.45,结果精确到0.1).