随着农业科技的不断发展,农田灌溉也开始采用喷灌的形式(如图甲).在田间安装一个离开地面一定高度且垂直于地面的喷头,喷头可旋转360°,喷出的水流呈抛物线形状.如图乙,用OA表示垂直于地面MN的喷头,OA=1m,水流在与OA的水平距离10m时达到最高点,这时最高点离地面5m.如果不计其他因素,当喷头环绕一周后,能喷灌的最大直径是多少米?(结果精确到0.1,参考数据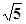 ≈2.236)
≈2.236)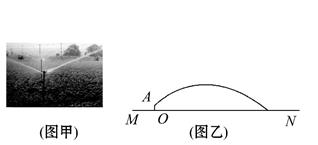
相关知识点
推荐套卷
随着农业科技的不断发展,农田灌溉也开始采用喷灌的形式(如图甲).在田间安装一个离开地面一定高度且垂直于地面的喷头,喷头可旋转360°,喷出的水流呈抛物线形状.如图乙,用OA表示垂直于地面MN的喷头,OA=1m,水流在与OA的水平距离10m时达到最高点,这时最高点离地面5m.如果不计其他因素,当喷头环绕一周后,能喷灌的最大直径是多少米?(结果精确到0.1,参考数据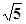 ≈2.236)
≈2.236)