“5.12”汶川地震发生后,某天广安先后有两批自愿者救援队分别乘客车和出租车沿
相同路线从广安赶往重灾区平武救援,下图表示其行驶过程中路程随时间的变化图象.
(1)根据图象,请分别写出客车和出租车行驶过程中路程与时间之间的函数关系式(不写出自变量的取值范围);(2)写出客车和出租车行驶的速度分别是多少?
(3)试求出出租车出发后多长时间赶上客车? 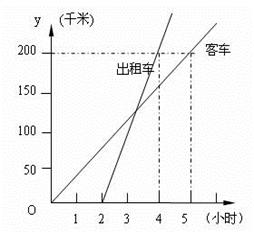
相关知识点
推荐套卷
“5.12”汶川地震发生后,某天广安先后有两批自愿者救援队分别乘客车和出租车沿
相同路线从广安赶往重灾区平武救援,下图表示其行驶过程中路程随时间的变化图象.
(1)根据图象,请分别写出客车和出租车行驶过程中路程与时间之间的函数关系式(不写出自变量的取值范围);(2)写出客车和出租车行驶的速度分别是多少?
(3)试求出出租车出发后多长时间赶上客车? 