已知，在△ABC中，AB=AC．过A点的直线a从与边AC重合的位置开始绕点A按顺时针方向旋转角θ，直线a交BC边于点P（点P不与点B、点C重合），△BMN的边MN始终在直线a上（点M在点N的上方），且BM=BN，连接CN．
（1）当∠BAC=∠MBN=90°时，
①如图a，当θ=45°时，∠ANC的度数为 ；
②如图b，当θ≠45°时，①中的结论是否发生变化？说明理由；
（2）如图c，当∠BAC=∠MBN≠90°时，请直接写出∠ANC与∠BAC之间的数量关系，不必证明．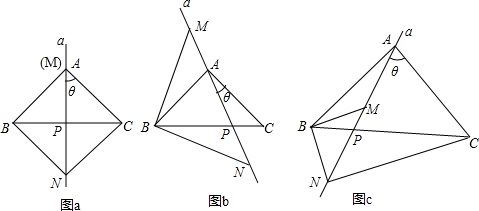
相关试题
，5，
，
，
，
，0，
，
，
，
在数轴上的对应点的位置填空。
0（2）
0 
0（4）
0
，
，
，
，
，
，……，观察规律，试猜想
的个位数是。如图，在梯形ABCD中，AD//BC，E是BC的中点，AD=5，BC=12，CD= 
，∠C=45°，点P是BC边上一动点，设PB的长为x。
（1）梯形ABCD的面积为_________；
（2）当x的值为___________时，以点P、A、D、E为顶点的四边形为直角梯形；
（3）当x的值为___________时，以点P、A、D、E为顶点的四边形为平行四边形；
（4）点P在BC边上运动的过程中，以P、A、D、E为顶点的四边形能否构成菱形？试说明理由。
GAE=450，相关知识点
推荐套卷
粤公网安备 44130202000953号