解答题:声音在空气中传播的速度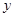 (m/s)是气温
(m/s)是气温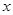 (℃)的一次函数,下表列出了一组不同气温的音速:
(℃)的一次函数,下表列出了一组不同气温的音速:
气温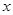 (℃) (℃) |
0 |
5 |
10 |
15 |
20 |
音速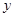 (m/s) (m/s) |
331 |
334 |
337 |
340 |
343 |
(1)求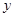 与
与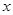 之间的函数关系式;(2)气温
之间的函数关系式;(2)气温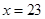 ℃时,某人看到烟花燃放5s后才听到声响,那么此人与烟花燃放地约相距多远?
℃时,某人看到烟花燃放5s后才听到声响,那么此人与烟花燃放地约相距多远?
相关知识点
推荐套卷
解答题:声音在空气中传播的速度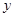 (m/s)是气温
(m/s)是气温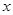 (℃)的一次函数,下表列出了一组不同气温的音速:
(℃)的一次函数,下表列出了一组不同气温的音速:
气温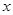 (℃) (℃) |
0 |
5 |
10 |
15 |
20 |
音速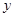 (m/s) (m/s) |
331 |
334 |
337 |
340 |
343 |
(1)求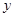 与
与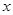 之间的函数关系式;(2)气温
之间的函数关系式;(2)气温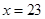 ℃时,某人看到烟花燃放5s后才听到声响,那么此人与烟花燃放地约相距多远?
℃时,某人看到烟花燃放5s后才听到声响,那么此人与烟花燃放地约相距多远?