(本小题满分14分)
已知点 、
、 ,(
,( )是曲线C上的两点,点
)是曲线C上的两点,点 、
、 关于
关于 轴对称,直线
轴对称,直线 、
、 分别交
分别交 轴于点
轴于点 和点
和点 ,
,
(Ⅰ)用 、
、 、
、 、
、 分别表示
分别表示 和
和 ;
;
(Ⅱ)某同学发现,当曲线C的方程为: 时,
时, 是一个定值与点
是一个定值与点 、
、 、
、 的位置无关;请你试探究当曲线C的方程为:
的位置无关;请你试探究当曲线C的方程为: 时,
时,  的值是否也与点M、N、P的位置无关;
的值是否也与点M、N、P的位置无关;
(Ⅲ)类比(Ⅱ)的探究过程,当曲线C的方程为 时,探究
时,探究 与
与 经加、减、乘、除的某一种运算后为定值的一个正确结论.(只要求写出你的探究结论,无须证明).
经加、减、乘、除的某一种运算后为定值的一个正确结论.(只要求写出你的探究结论,无须证明).
相关知识点
推荐套卷
 ,当
,当 时,
时,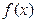 的极大值为7;当
的极大值为7;当 时,
时,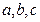 的值 ;(2)函数
的值 ;(2)函数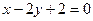 经过椭圆
经过椭圆 的左顶点
的左顶点
 和上顶点
和上顶点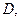 椭圆
椭圆 的右顶点为
的右顶点为 ,点
,点 是椭圆
是椭圆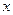 轴上方的动点,直线
轴上方的动点,直线 与直线
与直线 分别交于
分别交于 两点,如图所示。
两点,如图所示。 的长度的最小值;
的长度的最小值;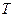 ,使得
,使得 的面积
的面积 ?若存在,确定点
?若存在,确定点 的图像如图所示。
的图像如图所示。
 在
在 处的切线方程为
处的切线方程为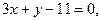 求函数
求函数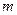 ,使得
,使得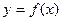 的图像与
的图像与
 。
。
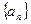 中,已知
中,已知 且
且 。
。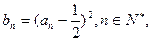 证明:数列
证明:数列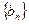 是等差数列,并求数列
是等差数列,并求数列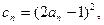 求
求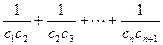 的值。
的值。 粤公网安备 44130202000953号
粤公网安备 44130202000953号