[福建]2011-2012年福建省四地六校高二第二次月考理科数学
从集合 中随机取出一个数,设事件
中随机取出一个数,设事件 为“取出的数为偶数”,事件
为“取出的数为偶数”,事件 为“取出的数为奇数”,则事件
为“取出的数为奇数”,则事件 与
与 ( )
( )
| A.是互斥且对立事件 | B.是互斥且不对立事件 |
| C.不是互斥事件 | D.不是对立事件 |
抛掷一枚质地均匀的硬币,如果连续抛掷1000次,那么第999次出现正面朝上的概率是( )
A. |
B. |
C. |
D. |
过抛物线 的焦点作直线
的焦点作直线 交抛物线于
交抛物线于 、
、 两点,若弦长
两点,若弦长 =8,则弦
=8,则弦 中点的横坐标为( )
中点的横坐标为( )
| A.1 | B.2 | C.3 | D.4 |
“双曲线方程为 ”是“双曲线离心率
”是“双曲线离心率 ”的 ( )
”的 ( )
| A.充要条件 | B.充分不必要条件 |
| C.必要不充分条件 | D.既不充分也不必要条件 |
如图是某赛季甲、乙两名篮球运动员每场比赛得分的茎叶图,则在这几场比赛中甲得分的中位数与乙得分的众数分别是( )
| A.3,2 | B.28,32 | C.23,23 | D.8,2 |

下列四个命题:
①使用抽签法,每个个体被抽中的机会相等;
②将十进制数 化为二进制数为
化为二进制数为 ;
;
③利用秦九韶算法
求多项式  在
在 的值时
的值时 ;
;
④已知一个线性回归方程是 ,则变量
,则变量 之间具有正相关关系.
之间具有正相关关系.
其中真命题的个数是 ( )
| A.1 | B.2 | C.3 | D.4 |
已知动点A、B分别在图中抛物线 及椭圆
及椭圆 的实线上运动,若
的实线上运动,若 ∥
∥ 轴,点N的坐标
轴,点N的坐标
为(1,0),则三角形ABN的周长 的取值范围是 ( )
的取值范围是 ( )
A. B.
B. C.
C. D.
D.
右图的矩形,长为5 m,宽为2 m,在矩形内随机地撒 300颗黄豆,数得落在阴影部分的黄豆数为138颗,则我们可以估计出阴影部分的面积为
300颗黄豆,数得落在阴影部分的黄豆数为138颗,则我们可以估计出阴影部分的面积为  ;
;
如图,P是双曲线 上的动点,
上的动点, 、
、 是双曲线的左右焦点,
是双曲线的左右焦点, 是
是 的平分线上一点
的平分线上一点 ,且
,且 某同学用以下方法研究
某同学用以下方法研究 :延长
:延长 交
交 于点
于点 ,可知
,可知 为等腰三角形,且M为
为等腰三角形,且M为 的中点,得
的中点,得 类似地:P是椭圆
类似地:P是椭圆 上的动点,
上的动点, 、
、 是椭圆的左右焦点,M是
是椭圆的左右焦点,M是 的平分线上一点,且
的平分线上一点,且 ,则
,则 的取值范围是 .
的取值范围是 .
(本题满分13分)
为了了解某校高中部学生的体能情况,体育组决定抽样三个年级部分学生进行跳绳测试,并将所得的数据整理后画出频率分布直方图.已知图中从左到右的前三个小组的频率分别是0.1,0.3,0.4,第一小组的频数是5.
(I) 求第四小组的频率和参加这次测试的学生人数;
(II) 在这次测试中,学生跳绳次数的中位数落在第几小组内?
(III) 参加这次测试跳绳次数在100次以上为优秀,试估计该校此年级跳绳成绩的优秀率是多少?

(本题满分13分)
把一颗骰子投掷两次,记第一次出现的点数为 ,第二次出现的点数为
,第二次出现的点数为 (其中
(其中 ).
).
(Ⅰ)若记事件 “焦点在
“焦点在 轴上的椭圆的方程为
轴上的椭圆的方程为 ”,求事件
”,求事件 的概率;
的概率;
(Ⅱ)若记事件 “离心率为2的双曲线的方程为
“离心率为2的双曲线的方程为 ”,求事件
”,求事件 的概率.
的概率.
(本小题满分13分)
已知抛物线 的顶点在原点,焦点为
的顶点在原点,焦点为 ,且过点
,且过点 .
.
(1)求t的值;
(2)若直线 与抛物线
与抛物线 只有一个公共点,求实数
只有一个公共点,求实数 的值.
的值.
(本小题满分13分)
设命题 :对任意实数
:对任意实数 ,不等式
,不等式 恒成立;命题
恒成立;命题 :方程
:方程 表示焦点在
表示焦点在 轴上的双曲线.
轴上的双曲线.
(I)若命题 为真命题,求实数
为真命题,求实数 的取值范围;
的取值范围;
(II)若命题“ ”为真命题,且“
”为真命题,且“ ”为假命题,求实数
”为假命题,求实数 的取值范围.
的取值范围.
(本小题满分14分)
已知中心在坐标轴原点O的椭圆C经过点A(1, ),且点F(-1,0)为其左焦点.
),且点F(-1,0)为其左焦点.
(I)求椭圆C的离心率;
(II)试判断以AF为直径的圆与以椭圆长轴为直径的圆的位置关系,并说明理由.
 的焦点坐标为 ( )
的焦点坐标为 ( ) )
) 与
与 (
( )的曲线大致是 ( )
)的曲线大致是 ( )
 ,
, ,c
,c ,则( )
,则( )



 .则
.则 是__________;
是__________;
 的渐近线方程式为
的渐近线方程式为 ,则
,则 等于
等于  的左焦点在抛物线
的左焦点在抛物线 的准线上,则p的值为_______;
的准线上,则p的值为_______; 、
、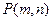 ,(
,( )是曲线C上的两点,点
)是曲线C上的两点,点 、
、 关于
关于 轴对称,直线
轴对称,直线 、
、 分别交
分别交 和点
和点 ,
, 、
、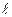 、
、 、
、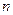 分别表示
分别表示 和
和 ;
;  时,
时,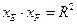 是一个定值与点
是一个定值与点 的位置无关;请你试探究当曲线C的方程为:
的位置无关;请你试探究当曲线C的方程为: 时,
时, 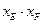 的值是否也与点M、N、P的位置无关;
的值是否也与点M、N、P的位置无关; 时,探究
时,探究 与
与 经加、减、乘、除的某一种运算后为定值的一个正确结论.(只要求写出你的探究结论,无须证明).
经加、减、乘、除的某一种运算后为定值的一个正确结论.(只要求写出你的探究结论,无须证明). 粤公网安备 44130202000953号
粤公网安备 44130202000953号