已知对任意的平面向量，把
绕其起点沿逆时针方向旋转
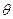角，得到向量
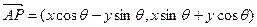，叫做把点B绕点A逆时针方向旋转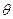角得到点P
①已知平面内的点A（1，2），B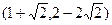
，把点B绕点A沿逆时针方向旋转
后得到点P，求点P的坐标
②设平面内曲线C上的每一点绕逆时针方向旋转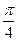
后得到的点的轨迹是曲线
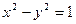，求原来曲线C的方程.
相关试题
与直线
相切，求实数a的值。
;
+
>
+
。
是该函数的一个极值点，求函数
的单调区间
上是单调减函数，求
的取值范围
的扇形，制成一个圆锥形容器，扇形的圆心角相关知识点
推荐套卷
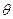已知对任意的平面向量，把绕其起点沿逆时针方向旋转角，得到向量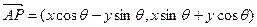，叫做把点B绕点A逆时针方向旋转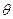角得到点P
①已知平面内的点A（1，2），B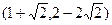，把点B绕点A沿逆时针方向旋转后得到点P，求点P的坐标
②设平面内曲线C上的每一点绕逆时针方向旋转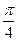后得到的点的轨迹是曲线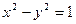，求原来曲线C的方程.
粤公网安备 44130202000953号