(本题满分16分)
已知函数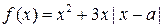 ,其中
,其中 ,
,
(1)当 时,把函数
时,把函数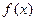 写成分段函数的形式;
写成分段函数的形式;
(2)当 时,求
时,求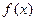 在区间
在区间 上的最值;
上的最值;
(3)设 ,函数
,函数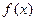 在
在 上既有最大值又有最小值,请分别求出
上既有最大值又有最小值,请分别求出 的取值范围(用
的取值范围(用 表示).
表示).
相关知识点
推荐套卷
(本题满分16分)
已知函数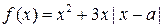 ,其中
,其中 ,
,
(1)当 时,把函数
时,把函数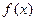 写成分段函数的形式;
写成分段函数的形式;
(2)当 时,求
时,求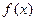 在区间
在区间 上的最值;
上的最值;
(3)设 ,函数
,函数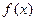 在
在 上既有最大值又有最小值,请分别求出
上既有最大值又有最小值,请分别求出 的取值范围(用
的取值范围(用 表示).
表示).