(本小题满分12分)(考生注意:本题请从以下甲乙两题中任选一题作答,若两题都答 只以甲题计分)
只以甲题计分)
甲:设数列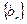 的前
的前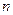 项和为
项和为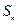 ,且
,且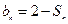 ;数列
;数列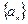 为等差数列,且
为等差数列,且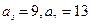
(Ⅰ)求数列 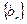 的通项公式
的通项公式
(Ⅱ)若 ,
,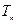 为数列
为数列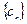 的前
的前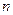
 项和,求
项和,求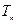
乙:定义在[-1,1]上的奇函数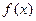 ,已知当
,已知当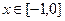 时,
时,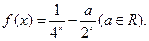
(Ⅰ)求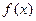 在[0,1]上的最大值
在[0,1]上的最大值
(Ⅱ)若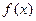 是[0,1]上的增函数,求实数
是[0,1]上的增函数,求实数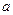 的取值范围
的取值范围
相关知识点
推荐套卷
(本小题满分12分)(考生注意:本题请从以下甲乙两题中任选一题作答,若两题都答 只以甲题计分)
只以甲题计分)
甲:设数列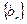 的前
的前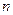 项和为
项和为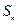 ,且
,且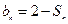 ;数列
;数列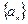 为等差数列,且
为等差数列,且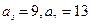
(Ⅰ)求数列 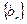 的通项公式
的通项公式
(Ⅱ)若 ,
,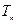 为数列
为数列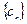 的前
的前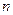
 项和,求
项和,求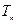
乙:定义在[-1,1]上的奇函数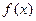 ,已知当
,已知当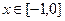 时,
时,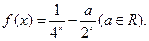
(Ⅰ)求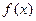 在[0,1]上的最大值
在[0,1]上的最大值
(Ⅱ)若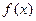 是[0,1]上的增函数,求实数
是[0,1]上的增函数,求实数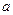 的取值范围
的取值范围