已知函数
f(x)=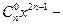
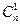
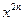
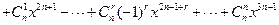 ,其中n
,其中n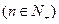 .
.
(1)求函数f(x)的极大值和极小值; (2)设函数f(x)取得极大值时x=
(2)设函数f(x)取得极大值时x=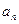 ,令
,令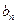 =2
=2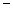 3
3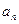 ,
,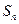 =
=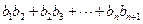 ,若p≤
,若p≤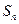 <q对一切n∈N+恒成立,求实数p和q的取值范围.
<q对一切n∈N+恒成立,求实数p和q的取值范围.
相关知识点
推荐套卷
已知函数
f(x)=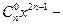
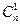
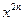
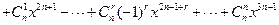 ,其中n
,其中n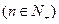 .
.
(1)求函数f(x)的极大值和极小值; (2)设函数f(x)取得极大值时x=
(2)设函数f(x)取得极大值时x=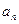 ,令
,令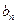 =2
=2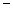 3
3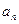 ,
,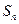 =
=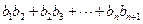 ,若p≤
,若p≤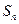 <q对一切n∈N+恒成立,求实数p和q的取值范围.
<q对一切n∈N+恒成立,求实数p和q的取值范围.