（（本题14分）定义：若函数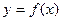
在某一区间D上任取两个实数
、
，且
，都有
，则称函数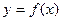在区间D上具有性质L。
（1）写出一个在其定义域上具有性质L的对数函数（不要求证明）。
（2）对于函数
，判断其在区间
上是否具有性质L？并用所给定义证明你的结论。
（3）若函数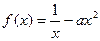
在区间（0，1）上具有性质L，求实数
的取值范围。
与点
的距离比它到直线
的距离小1，求点
、
、
,且
.
的值;
,求
面积的最大值.
的最大值不大于
，又当
，求
的值。
在区间
内有一最大值
，求
的值.
时，求函数
的最小值。相关知识点
推荐套卷
（（本题14分）定义：若函数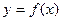在某一区间D上任取两个实数、，且，都有，则称函数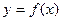在区间D上具有性质L。
（1）写出一个在其定义域上具有性质L的对数函数（不要求证明）。
（2）对于函数，判断其在区间上是否具有性质L？并用所给定义证明你的结论。
（3）若函数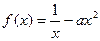在区间（0，1）上具有性质L，求实数的取值范围。
粤公网安备 44130202000953号