(本小题满分12分)已知二次函数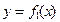 的
的 图象以原点为顶点且过点(1,1),反比例函数
图象以原点为顶点且过点(1,1),反比例函数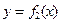 的图象与直线
的图象与直线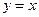 的两个交点间的距离为8,
的两个交点间的距离为8,
(1)求函数 的表达式;
的表达式;
(2)证明:当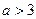 时,关于
时,关于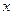 的方程
的方程 有三个实数解.
有三个实数解.
相关知识点
推荐套卷
(本小题满分12分)已知二次函数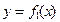 的
的 图象以原点为顶点且过点(1,1),反比例函数
图象以原点为顶点且过点(1,1),反比例函数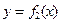 的图象与直线
的图象与直线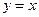 的两个交点间的距离为8,
的两个交点间的距离为8,
(1)求函数 的表达式;
的表达式;
(2)证明:当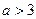 时,关于
时,关于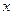 的方程
的方程 有三个实数解.
有三个实数解.