已知二次函数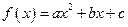 满足条件:①
满足条件:① 是
是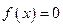 的两个零点;②
的两个零点;②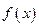 的最小值为
的最小值为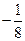
(1)求函数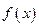 的解析式;
的解析式;
(2)设数列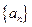 的前
的前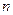 项积为
项积为 ,且
,且 ,
,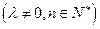 ,求数列
,求数列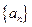 的前
的前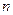 项和
项和
(3)在(2)的条件下,当 时,若
时,若 是
是 与
与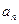 的等差中项,试问数列
的等差中项,试问数列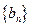 中
中
第几项的值最小?并求出这个最小值。
相关知识点
推荐套卷
已知二次函数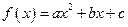 满足条件:①
满足条件:① 是
是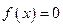 的两个零点;②
的两个零点;②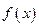 的最小值为
的最小值为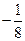
(1)求函数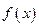 的解析式;
的解析式;
(2)设数列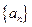 的前
的前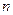 项积为
项积为 ,且
,且 ,
,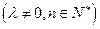 ,求数列
,求数列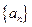 的前
的前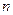 项和
项和
(3)在(2)的条件下,当 时,若
时,若 是
是 与
与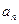 的等差中项,试问数列
的等差中项,试问数列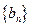 中
中
第几项的值最小?并求出这个最小值。