(本小题满分6分)
已知:二次函 数y=
数y= x²
x² +bx+c,其图象对称轴为直线x=1,且经过点(2,–
+bx+c,其图象对称轴为直线x=1,且经过点(2,– ).
).
(1)求此二次函数的解析式.
(2)设该图象与x轴交于B、C两点(B点在C点的左侧),请在此二次函数x轴下方的图
象上确定一点E,使△EBC的面积最大,并求出最大面积.
注:二次函数y= x2+bx+c(
x2+bx+c( ≠0)的对称轴是直线x=-
≠0)的对称轴是直线x=-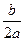 .
.
相关知识点
推荐套卷
(本小题满分6分)
已知:二次函 数y=
数y= x²
x² +bx+c,其图象对称轴为直线x=1,且经过点(2,–
+bx+c,其图象对称轴为直线x=1,且经过点(2,– ).
).
(1)求此二次函数的解析式.
(2)设该图象与x轴交于B、C两点(B点在C点的左侧),请在此二次函数x轴下方的图
象上确定一点E,使△EBC的面积最大,并求出最大面积.
注:二次函数y= x2+bx+c(
x2+bx+c( ≠0)的对称轴是直线x=-
≠0)的对称轴是直线x=-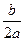 .
.