(12分)已知等差数列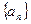
中，前n项和
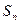满足：
，
。
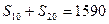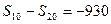(Ⅰ)求数列的通项公式以及前n项和公式。
（Ⅱ）是否存在三角形同时具有以下两个性质，如果存在请求出相应的三角形三边
以及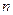
和
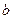值：
（1）三边是数列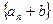
中的连续三项，其中
；
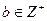（2）最小角是最大角的一半。
的两条对角线相交于点
，
边所在直线的方程为
, 点
在
边所在直线上．
的顶点A为（3，－1），AB边上的中线所在直线方程为
，
的平分线所在直线方程为
，求BC边所在直线的方程．
在下列条件下求
的值.
;
;
相关知识点
推荐套卷
(12分)已知等差数列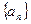中，前n项和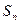满足：，。
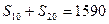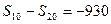(Ⅰ)求数列的通项公式以及前n项和公式。
（Ⅱ）是否存在三角形同时具有以下两个性质，如果存在请求出相应的三角形三边
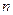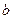以及和值：
（1）三边是数列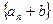中的连续三项，其中；
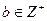（2）最小角是最大角的一半。
粤公网安备 44130202000953号