(本小题满分12分)
我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市政府为了节约生活用水,计划在本市试行居民生活用水定额管理,为此市政府首先采用抽样调查的方法获得了 位居民某年的月均用水量(单位:吨).根据所得的
位居民某年的月均用水量(单位:吨).根据所得的 个数据按照区间
个数据按照区间 进行分组,得到频率分布直方图如图
进行分组,得到频率分布直方图如图
(1)若已知 位居民中月均用水量小于1吨的人数是12,求
位居民中月均用水量小于1吨的人数是12,求 位居民中月均用水量分别在区间
位居民中月均用水量分别在区间 和
和 内的人数;
内的人数;
(2)在该市居民中随意抽取10位,求至少有2位居民月均用水量在区间 或
或 内的概率.(精确到0.01.参考数据:
内的概率.(精确到0.01.参考数据: )
)
相关知识点
推荐套卷
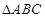 中,角A、B、C的对边分别为a、b、c,且角A、B、C成等差教列.(1)若
中,角A、B、C的对边分别为a、b、c,且角A、B、C成等差教列.(1)若 ,求边c的值;
,求边c的值;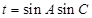 ,求t的最大值.
,求t的最大值.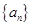 的首项
的首项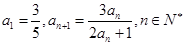 .
.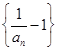 为等比数列;
为等比数列;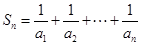 ,若
,若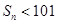 ,求最大正整数
,求最大正整数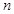 的值;
的值;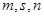 ,使
,使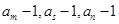 成等比数列?如果存在,请给予证明;如果不存在,请说明理由.
成等比数列?如果存在,请给予证明;如果不存在,请说明理由. }的首项为
}的首项为 a
a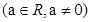 .设数列的前n项和为Sn,且对任意正整数n都有
.设数列的前n项和为Sn,且对任意正整数n都有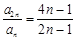 .
.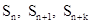 成等比数列?若存在,求出n和k的值;若不存在,请说明理由.
成等比数列?若存在,求出n和k的值;若不存在,请说明理由.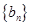 中的
中的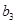 、
、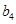 、
、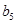 .
.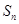 ,求证:数列
,求证:数列 是等比数列.
是等比数列.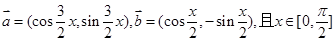 ,
,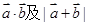 ;
;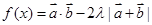 的最小值是
的最小值是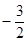 ,求实数
,求实数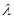 的值.
的值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号