某食品厂为了检查一条自动包装流水线的生产情况，随机抽取该流水线上的40件产品作为样本称出它们的重量（单位：克），重量的分组区间为（490,495]，（495,500]，……，（510,515]，由此得到样本的频率分布直方图，如图4所示.根据频率分布直方图，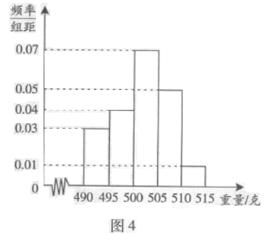
求（1）重量超过500 克的产品的频率；
（2）重量超过500 克的产品的数量.
相关试题
满足
，
．
求
的最大项和最小项的值．
的通项公式；
的前
项和为
，
．已知
，
，
，且当
时，
．
的值；
为等比数列；
是递增的等比数列，且
为数列
，求数列
的前n项和
．
}是等差数列；相关知识点
推荐套卷
某食品厂为了检查一条自动包装流水线的生产情况，随机抽取该流水线上的40件产品作为样本称出它们的重量（单位：克），重量的分组区间为（490,495]，（495,500]，……，（510,515]，由此得到样本的频率分布直方图，如图4所示.根据频率分布直方图，
求（1）重量超过500 克的产品的频率；
（2）重量超过500 克的产品的数量.
粤公网安备 44130202000953号