甲、乙、丙三名射击选手，各射击一次，击中目标的概率如下表所示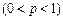
：
| 选手 |
甲 |
乙 |
丙 |
| 概率 |
 |
 |
|
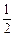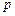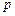若三人各射击一次，恰有k名选手击中目标的概率记为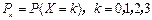
．
(1) 求X的分布列；（2）若击中目标人数的均值是2，求P的值．
中，
的取值范围.
中，若
，设
，
是等比数列；
是公比为
的等比数列，推导
项公式.
满足：
，
.
的各项均为正数，
为其前
项和，若
，
，求
，
，
，求B及S
.推荐套卷
甲、乙、丙三名射击选手，各射击一次，击中目标的概率如下表所示：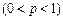
| 选手 |
甲 |
乙 |
丙 |
| 概率 |
|
|
|
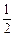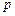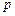若三人各射击一次，恰有k名选手击中目标的概率记为．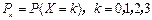
(1) 求X的分布列；（2）若击中目标人数的均值是2，求P的值．
粤公网安备 44130202000953号