（本大题满分14分)
如图，已知直线L：
过椭圆C：
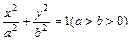的右焦点F，
且交椭圆C于A、B两点，点A、B在直线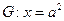
上的射影依次为点D、E.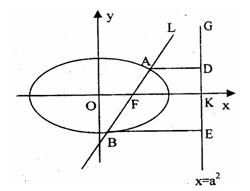
（Ⅰ）若抛物线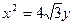
的焦点为椭圆C的上顶点，求椭圆C的方程；
（Ⅱ）若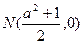
为x轴上一点；
求证: A、N、E三点共线.
相关试题
，求
的值；（2）如果
，求
的取值范围．
的图象与
轴交于点
，且最小正周期为π．
和
的值；（2）已知点
，点
是该函数图象上一点，点
是
的中点，当
，
时，求
的值．
（其中
）（1）求函数
的值域； （2）若函数
的图象与直线
的两个相邻交点间的距离为
，求函数
是三角形
三内角，向量
，且
；（Ⅱ）若
，求
）是函数
且
）的图象上一点，等比数列
的前
项和为
,数列
的首项为
，且前
满足
=
+
（
）.
前
，问
的最小正整数推荐套卷
（本大题满分14分)
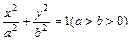如图，已知直线L：过椭圆C：的右焦点F，
且交椭圆C于A、B两点，点A、B在直线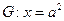上的射影依次为点D、E.
（Ⅰ）若抛物线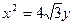的焦点为椭圆C的上顶点，求椭圆C的方程；
（Ⅱ）若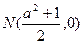为x轴上一点；
求证: A、N、E三点共线.
粤公网安备 44130202000953号