（本小题满分14分）
已知A（-1，2）为抛物线C: y=2x2上的点，直线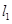
过点A，且与抛物线C 相切，直线
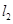:x=a(a≠-1)交抛物线C于B，交直线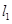于点D.
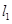（1）求直线的方程.
（2）设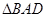
的面积为S1，求
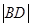及S1的值.
（3）设由抛物线C，直线
所围成的图形的面积为S2，求证S1:S2的值为与a无关的常数.
相关试题
中，
平面
，四边形
，
分别是
，
的中点．若
，
。
平面
；
平面
和
满足
，
，
。
为等差数列,并求数列
项和为
，令
,求
的最小值。
。
的周期和及其图象的对称中心；
，满足
求函数
的取值范围。
：
，
：
， 且
的取值范围。
，若
对一切
恒成立．求实数
的取值范围．相关知识点
推荐套卷
（本小题满分14分）
已知A（-1，2）为抛物线C: y=2x2上的点，直线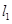过点A，且与抛物线C 相切，直线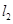:x=a(a≠-1)交抛物线C于B，交直线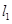于点D.
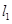（1）求直线的方程.
（2）设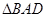的面积为S1，求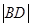及S1的值.
（3）设由抛物线C，直线所围成的图形的面积为S2，求证S1:S2的值为与a无关的常数.
粤公网安备 44130202000953号