请考生在第22、23、24三题中任选一题作答,如果多做,则按所做的第一题记分.
(本小题满分10分)选修4—1:几何证明选讲
如图,AB是⊙O的直径,弦BD、CA的延长线相交于
点E,EF垂直B A的延长线于点F. 求证:
A的延长线于点F. 求证:
(Ⅰ)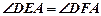 ;
;
(Ⅱ)

相关知识点
推荐套卷
请考生在第22、23、24三题中任选一题作答,如果多做,则按所做的第一题记分.
(本小题满分10分)选修4—1:几何证明选讲
如图,AB是⊙O的直径,弦BD、CA的延长线相交于
点E,EF垂直B A的延长线于点F. 求证:
A的延长线于点F. 求证:
(Ⅰ)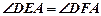 ;
;
(Ⅱ)
