三、解答题：（本大题共6小题，共75分，解答应写出文字说明、证明过程或演算步骤．）
16. （本小题满分12分）
已知向量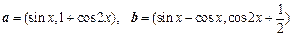
，定义函数
（Ⅰ）求函数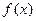
最小正周期；
（Ⅱ）在△ABC中,角A为锐角，且
，求边AC的长．
按从小到大的顺序排列.
的值域.
，相关知识点
推荐套卷
三、解答题：（本大题共6小题，共75分，解答应写出文字说明、证明过程或演算步骤．）
16. （本小题满分12分）
已知向量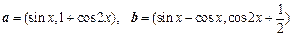，定义函数
（Ⅰ）求函数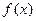最小正周期；
（Ⅱ）在△ABC中,角A为锐角，且，求边AC的长．
粤公网安备 44130202000953号