如图,已知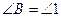 ,
, 是△
是△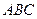 的角平分线,求证:
的角平分线,求证: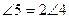 .请在下面横线上填出推理的依据:
.请在下面横线上填出推理的依据:
证明:∵ 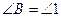 ,(已知)
,(已知)
∴  ∥
∥ .(同位角相等、两直线平行)
.(同位角相等、两直线平行)
∴ 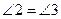 .( )
.( )
∵  是△
是△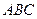 的角平分线,( )
的角平分线,( )
∴  . ( )
. ( )
∴  . ( )
. ( )
∵  ,(三角形的一个外角等于与它不相邻的两个内角和)
,(三角形的一个外角等于与它不相邻的两个内角和)
∴ 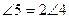 . ( 等量代换 )
. ( 等量代换 )
相关知识点
推荐套卷


 ,且
,且 ,
, ,
, .求证:BC∥EF.
.求证:BC∥EF.

 ( )
( ) ( )
( ) (已知)
(已知) (不写作法,保留作图痕迹)求作:∠
(不写作法,保留作图痕迹)求作:∠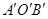 ,使得∠
,使得∠ ∠
∠
 粤公网安备 44130202000953号
粤公网安备 44130202000953号